Loading

Loading JML Contracts

In this chapter, we first explain how to load a Java program into KeY, and then introduce you to KeY's logic using the program you just loaded.

The example program used in this and the following chapter can be downloaded here.

Scenario

The tutorial example is a small paycard application consisting of two packages paycard and gui. The paycard package contains all classes implementing the program logic and has no dependencies to the gui package.

paycard consists of the classes: PayCard, LogFile, and LogRecord. gui package contains ChargeUI, IssueCardUI, and the main class Start.

In order to compile the project, change to the quicktour-2.0 directory and execute the following command:

javac -sourcepath . gui/*.java

Executing

java -classpath . gui.Start

starts the application. Try this now¹.

The first dialog when executing the main method in Start asks the customer (i.e., the user of the application) to obtain a paycard. A paycard can be charged by the customer with a certain amount of money and thereafter used for cashless payment until the pre-loaded money is eaten up.

To prevent any risk to the customer when losing the paycard, there is a limit up to which money can be loaded or charged on the paycard. There are three paycard variants with different limits: a standard paycard with a limit of 1000, a junior paycard with a limit of 100, or a paycard with a user-defined limit. The initial balance of a newly issued paycard is zero.

In the second dialog coming up after obtaining a paycard, the customer may charge their paycard with a certain amount of money. But the charge operation is only successful if the current balance of the paycard plus the amount to charge is less than the limit of the paycard. Otherwise, i.e., if the current balance plus the amount to charge is greater or equal the limit of the paycard, the charge operation does not change the balance on the paycard and an attribute counting unsuccessful operations is increased.

The KeY tool aims to formally prove that the implementation actually satisfies such requirements. For example, one can formally verify the invariant that the balance on the paycard is always less than the limit of the paycard.

The intended semantics of some classes is specified with the help of invariants denoted in the Java Modeling Language (JML) ¹². Likewise, the behavior of most methods is described in form of pre- and postconditions in JML. We do not go into details on how JML specifications for Java classes are created. The tools downloadable from http://jmlspecs.org/download.shtml may be helpful here. In particular, we require and assume that all JML specifications are complying to the JML standards ¹. KeY's JML front-end is no substitute for the JML parser / type checker.

A First Look on the JML Specification

Before we can verify that the program satisfies the property mentioned in the previous section, we need to express it in JML. The remaining section tries to give a short, intuitive impression on what such a specification looks like. In Sect. 3, JML specifications are explained in a bit more depth.

Load the file paycard/PayCard.java in an editor of your choice and search for the method isValid. You should see something like

        /*@
          @ public normal_behavior
          @ requires true;
          @ ensures \result == (unsuccessfulOperations<=3); 
          @ assignable \nothing;
          @*/
        public /*@pure@*/ boolean isValid() {
           if (unsuccessfulOperations<=3) {
              return true;
           } else {
              return false;
           }
        }

JML specifications are annotated as special marked comments in Java files. Comments containing JML annotations have an "at" sign directly after the comment sign as a start marker and---for multi-line comments---also as an end marker.

The JML annotation in the above listing represents a JML method contract. A contract states that when the caller of a method ensures that certain conditions (precondition + certain invariants (see Sect. 4{reference-type="ref" reference="sec:provableProp"})) then the method ensures that after the execution the postcondition holds².

The precondition is true. This means the precondition does not place additional conditions the caller has to fulfill in order to be guaranteed that after the execution of the method its postcondition holds, though there might be conditions stemming from invariants.

The ensures clause specifies the method's postcondition and states simply that the return value of the method is true if and only if there have not been more than 3 unsuccessful operations. Otherwise, false is returned.

For the other parts of the method specification, see Sect. 4{reference-type="ref" reference="sec:provableProp"}.

How to Verify JML Specifications with the KeY tool

JML specifications, in particular pre- and postconditions, can be seen as abstractions of an implementation. In this context, an implementation is called correct if it actually implies the properties expressed in its specification. The KeY tool includes functionality to verify the correctness of an implementation with respect to its specification.

In this section, we describe how to start (Sect. 3.1{reference-type="ref" reference="sec:starting"}) the KeY prover and load the tutorial example (Sect. 3.2{reference-type="ref" reference="sec:loading"}) as well as a short overview about the graphical user interface and its options (Sect. 3.3). Last but not least, we explain how to configure the KeY prover to follow the tutorial example (Sect. 3.4{reference-type="ref" reference="sec:configure"}).

Starting the KeY prover

In order to verify a program, you first need to start the KeY prover. This is done either by using the webstart mechanism (see Sect. 1.2.1{reference-type="ref" reference="install:javaws"}) or by running the jar file from your KeY distribution³, e.g., by running

java -jar key.jar

Loading the Tutorial Example

After downloading and unpacking this quicktour, you should find a directory containing the two subdirectories paycard and gui. We refer to the directory jml as top-level directory.

1. You have to choose the Java source files you want to verify. They contain both the source code and the JML annotations. You can do this by either

   • adding the path to the paycard directory to the command:

     java -jar key.jar <path‘_to‘_quicktour>/jml/paycard

   • opening [File] $|$ [Load] and selecting the paycard package directory after having started KeY without any arguments.

   KeY will then load the tutorial example and parse the JML annotations. If you get an error dialog similar to the one in Fig. 1{reference-type="ref" reference="fig:error:unknownType"}, you have selected the jml directory instead of its subdirectory paycard.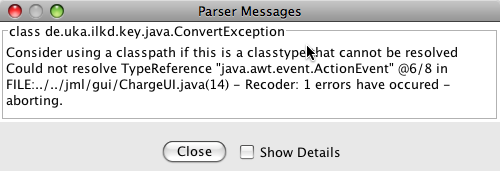

   {#fig:error:unknownType width="75%"}

   If you have your own projects you want to verify, you can proceed similarly. Please note that KeY by default supports only a very limited selection of the standard library classes. How to extend them and how to configure more complex projects that use 3^rd party libraries is described in brief in App. 9{reference-type="ref" reference="app:configuringProjects"}.

2. Now the Proof Management window should appear as shown in Fig. [fig:pob:startup]{reference-type="ref" reference="fig:pob:startup"}.

   In the left part of the window titled [Contract Targets], the Proof Management lists all packages, classes, interfaces, and methods of the project to be verified in a tree structure similar to standard file managers.

   The browser allows you to select the proof obligation you want to verify. Selecting PayCard::charge gives you three contracts (Fig. [fig:pob:expandedProofObligations]{reference-type="ref" reference="fig:pob:expandedProofObligations"}): one [exceptional_behavior] and two [normal_behavior] contracts. Select the first [normal_behavior] contract and confirm by pressing the button [OK]. More details about the contract configurator will be given in Sect. 4{reference-type="ref" reference="sec:provableProp"}.

3. You should now see the KeY prover window with the loaded proof obligation as in Fig. 2{reference-type="ref" reference="fig:proverWithLoadedPO"}. The prover is able to handle predicate logic as well as dynamic logic. The KeY prover was developed as a part of the KeYproject and is implemented in [Java]{.smallcaps}. It features interactive application of proof rules as well as automatic application controlled by strategies. In the near future more powerful strategies will be available.

   In Sect. 4.3{reference-type="ref" reference="sec:application"}, we show how to prove some of the proof obligations generated for the tutorial example.

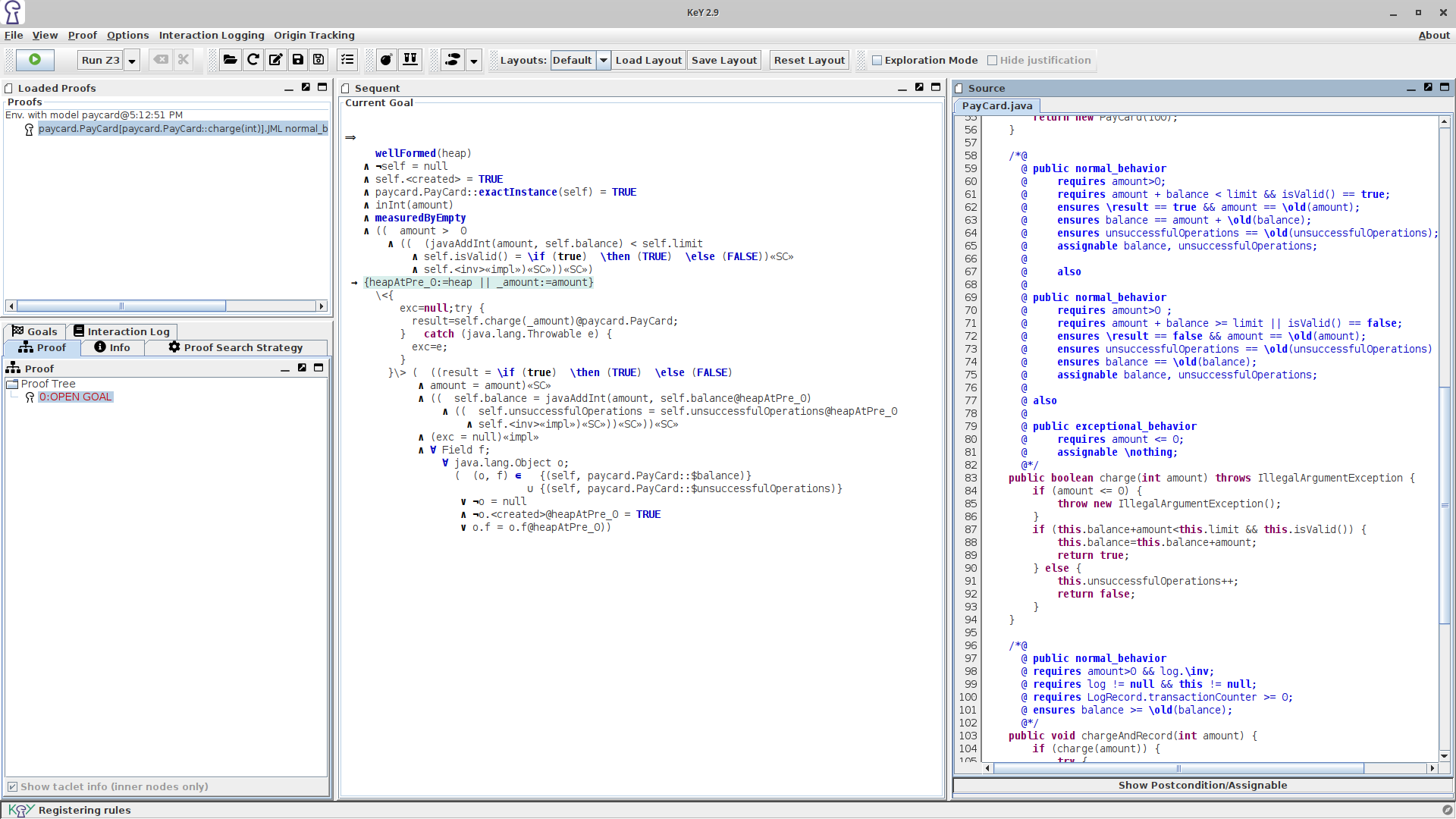{#fig:proverWithLoadedPO width="\textwidth"}

The KeY prover

We assume that you have performed the steps described in the previous section and that you see now something similar to Fig. 2{reference-type="ref" reference="fig:proverWithLoadedPO"}. In this section, we describe the GUI of the KeY tool and its different components. Most of the components in the GUI are also labeled with a tooltip.

The KeY prover window consists of a menubar, a toolbar (all buttons explained in 8{reference-type="ref" reference="app:shortcuts"}) and three panes where the lower left pane is additionally tabbed. Each pane is described below. The layout of the three panes can be changed by the user. Layouts can be saved and loaded in the [View] $|$ [Layout] menu.

• Upper left pane: Every problem you want to prove with the KeY prover is loaded in a proof environment. In this pane, all currently loaded problems respectively their proof environments are listed.

• Lower left pane: This pane contains the following five tabs.

  • Proof: This pane (see Fig. [fig:prover:tab:proof]{reference-type="ref" reference="fig:prover:tab:proof"}) contains the whole proof tree which represents the current proof. The nodes of the tree correspond to sequents (goals) at different proof stages. Click on a node to see the corresponding sequent and the rule that was applied on it in the following proof step (except if the node is a leaf). Leaf nodes of an open proof branch are colored red whereas leaves of closed branches are colored green.

    Pressing the right mouse button on a node of the proof tree will open a pop-up context menu. If you choose Prune Proof, the proof tree will be cut off at this node and all nodes lying below will be deleted. Choosing Apply Strategy will start an automatic proof search (see later Automatic Proving), but only on the branch which the node you had clicked on belongs to.

    The context menu also contains commands that allow you to hide closed subtrees, to hide inner nodes, to collapse, or to expand the tree. The commands help you to keep track of a large proof.

  • Goals: In this pane, the open goals of a certain proof (corresponding to one entry in the upper left pane) are listed. To work on a certain goal just click on it and the selected sequent will be shown in the right pane.

  • Info: In this pane (Fig. [fig:prover:tab:rules]{reference-type="ref" reference="fig:prover:tab:rules"}), all the rules, term labels, and function symbols available in the system are indicated.

    For the rules, KeY distinguishes between axiomatic taclets (rules that are always true in the given logic), lemmas (that are derived from and thus provable by axiomatic taclets) and built-in rules (for example how certain expressions can be simplified).

    By clicking on a rule of the list, the description of that rule is shown in the box below the rule list.

    Term labels are additional information that can be attached to a term. They do not change a term's semantics, but are used to guide the poof search or to carry non-logical information about a term, like its corresponding line number in the source code.

    The function symbols folder lists all interpreted function and predicate symbols in the dynamic logic.

  • Proof Search Strategy: This tab (see Fig. [fig:prover:tab:strategy]{reference-type="ref" reference="fig:prover:tab:strategy"}) allows you to define the active strategy from a set of available strategies. There are several parameters and only the most important ones will be covered here, a complete list can be found in 7{reference-type="ref" reference="app:strategy"}:

    • Max. Rule Applications: You can set the number $N_{aut}$ of automatic rule applications using the slider. Even if the automatic strategy can still apply rules after $N_{aut}$ applications, automatic proving stops.

    • Stop At: Choose when strategy execution shall stop. Possible values are Default: strategy stops when no rules are applicable or the maximal number of steps is reached and Unclosable: strategy stops in all situations when Default stops but also already when the first goal is encountered on which no further rule is (automatically) applicable.

    • Proof splitting: Influences usage of rules branching a proof tree. Only rules working on formulas not on programs fall under the chosen policy, i.e., program rules causing splits are still applied even if splitting is switched off. The values are free (withour restrictions), Delayed (allows still splitting but prefers other rules) and Off (no splitting).

    • Loop treatment: This setting determines how while-loops are treated. They can be left untouched (None), handled using stated invariant contracts, or repeatedly unrolled (Expand). If handled using invariants, you can either choose the new Loop Scope rule (recommended), or the legacy Transformation-based rule.

    • Method treatment: Methods can also be left untouched (None), have their method contracts applied (Contracts), or be inlined, i.e. have the method body expanded in place (Expand).

    • Dependency contract: For the simplification of heap terms, setting this option to On the information in JML's accessible clause is used.

    • Arithmetic treatment The KeY prover has several options for the treatment of arithmetic expressions:

      • Basic: Using this option, polynomial expressions are simplified. In the antecedent Gröbner Bases are computed polynomials. Linear inequations are handled using (partial) Omega procedures.

      • DefOps: Using the option [DefOps], mathematical symbols such as: /, %, jdiv, jmod, range predicates, such as int_RANGE, short_MIN and symbols for mathematical operations on integers with a certain semantic such as addJint or mulJshort, are expanded. This means for example constants, such as short_MIN, are replaced by their concrete values (in this case -32768) and range predicates, such as inInt are replaced by their ranges (in this case $i \leq int_{MAX} \wedge int_{MIN} \leq i$).

      • Model Search: Setting the [model search] option, the KeY prover supports non-linear equations and model search. Additionally multiplication of inequations with each other and systematic case distinctions (cuts) can be performed. This method is guaranteed to find counterexamples for invalid goals that only contain polynomial (in)equations. Such counterexamples turn up as trivially unprovable goals. It is also able to prove many more valid goals involving (in)equations, but will in general not terminate on such goals.

    • Quantifier treatment: Sometimes quantifiers within the sequent have to be instantiated. This can be either done manually (None) or automatically with different alternatives:

      • No Splits: Instantiate a quantifier only if this will not cause the proof to split.

      • Unrestricted: Instantiates a quantifier even when causing splits. However the startegy tries to predict the number of caused open branches and will prefer those with no or only few splits.

      • No Splits with Progs: Chooses between the No Splits and Unrestricted behaviour depending on programs present in the sequent. If a program is still present the No splits behaviour is used. Otherwise quantifiers are instantiated unrestricted

• Middle pane: In this pane, you can either inspect inner, already processed, nodes of the proof tree or you can continue the proof by applying rules to the open goals, whichever you choose in the left pane.

Rules can be applied either interactively or non-interactively using strategies:

• Interactive Proving: By moving the mouse over the current goal you will notice that a subterm of the goal is highlighted (henceforth called the focus term). Pressing the left mouse button displays a list of all proof rules currently applicable to the focus term.

  A proof rule is applied to the focus term simply by selecting one of the applicable rules and pressing the left mouse button. The effect is that a new goal is generated. By pushing the button Goal Back in the main window of the KeY prover it is possible to undo one or several rule applications. Note, that it is currently not possible to backtrack from an already closed goal.

• Automatic Proving: Automatic proof search is performed applying so-called strategies which can be seen as a collection of rules suited for a certain task. To determine which strategy should be used select the tab item Proof Search Strategy in the left pane as described above.

  To start (respectively continue) the proof push the run strategy-button on the toolbar labelled with the $\rhd$-symbol.

• Right pane: In this pane, you can see the Java source files pertaining to the currently selected proof. When mousing over a term in the middle pane, the corresponding JML specification in the right pane is highlighted in orange. As you advance in the proof, the source code line corresponding to the current proof state is highlighted in green.

Configure the KeY prover

In this section, we explain how to configure the KeY prover to follow the tutorial and give a few explanations about the implications of the chosen options. Most of the options are accessible via the KeY prover menu. An exhaustive list is available as part of Appendix 6{reference-type="ref" reference="app:menuOptions"}. In order to verify or change some of the necessary options, it is necessary to have a proof obligation loaded into the KeY prover as described in Sect. 3.2.

The menu bar consists of different pull-down menus: * File: menu for file related actions like loading and saving of problems resp. proofs, or opening the Proof Management window * View: menu for changing the look of the KeY prover * Proof: menu for changing and viewing proof specific options * Options: menu for configuring general options affecting any proof * About: menu (as the name says)

KeY provides a complete calculus for the Java Card 2.2.x version including additional features like transactions. Further, it provides some more concepts of real Java like class and object initialization. This quicktour is meant to help with the first steps in the system.

For simplicity, we deactivate some advanced concepts and configure the KeY prover to use the normal arithmetic integers to model Java integer types, which avoids dealing with modulo arithmetics. Important: Please note that this configuration is unsound with respect to the Java semantics.

In order to configure the KeY prover in this way, select [Options] $|$ [Show Taclet Options]. The dialog shows a list of available options. Clicking on an option in the list also shows a short explanation for the option. The list below explains the options necessary for this tutorial⁴. Please ensure that for each option, the value as given in parentheses directly after the option name is selected. In case you have to change one or more values, you will have to reload the tutorial example in order to activate them.

• JavaCard: ([off]) There are two values for this option: [on] and [off]. Switches all taclets axiomatising JavaCard specific features like transaction on or off.

• initialisation:

([disableStaticInitialisation]) Specifies whether static initialization should be considered.

intRules:

([arithmeticSemanticsIgnoringOF]) Here you can choose between
different semantics for Java integer arithmetic (for details
see [^3][^4][^5]). Three choices
are offered:

[javaSemantics]

:   (Java semantics): Corresponds exactly to the semantics defined
    in the Java language specification. In particular this means,
    that arithmetical operations may cause over-/underflow. This
    setting provides correctness but allows over-/underflows causing
    unwanted side-effects.

[arithmeticSemanticsIgnoringOF]

:   (Arithmetic semantics ignoring overflow): Treats the primitive
    finite Java types as if they had the same semantics as
    mathematical integers with infinite range. Thus this setting
    does not fulfil the correctness criteria.

[arithmeticSemanticsCheckingOF]

:   (Arithmetic semantics prohibiting overflow): Same as above but
    the result of arithmetical operations is not allowed to exceed
    the range of the Java type as defined in the language
    specification. This setting not only enforces the java semantics
    but also ascertains that no overflow occur.

Please activate Minimize Interaction in the Options menu in order reduce interaction with the system.

As a last preparation step, change to the [Proof Search Strategy] tab in the lower left pane and choose the following setting:

• [Max. Rule Applications] should be set to a value greater or equal 500. A too low value will cause the prover to leave automatic mode too early. In that case, you might have to press the run strategy button more often than described in the tutorial.

• [Java DL] must be selected with the following sub options:

  • Stop at: [Default]

  • Proof splitting: [Delayed] ([Normal] should also work)

  • Loop treatment: [Invariant (Loop Scope)]

  • Method treatment: [Expand]

  • Query treatment: [Expand]

  • Expand Local Queries: [On]

  • Arithmetic treatment: [Basic] is sufficient for this tutorial (when using division, modulo or similar you will need at least [DefOps])

  • Quantifier treatment: [No Splits with Progs] is a reasonable choice for most of the time

  • User-specific taclets: all [Off]

Provable properties

In the following, the ideas behind the various options for verification are described informally. A formal description of the generated proof obligations is contained in ⁶. For further details on the mapping between JML specifications and the formulas of the JavaDL logic used in KeY, please consult ⁷.

Examples of usage within the context of the case study in this tutorial are described in Sect. 4.3{reference-type="ref" reference="sec:application"}.

Informal Description of Proof Obligations

The current implementation of the KeY prover generates two kinds of proof obligations: functional contracts and dependency contracts⁵. Method contracts describe the behavior of a method. Properties covered by method contracts include:

• properties for method specifications: we show that a method fulfills its method contract,

• properties for class/object specifications: we show that a method preserves invariants of the object on which the call is invoked.

For the verification of programs, dependency contracts are used to be able to rely on the properties of, e.g. the object invariant, in parts of the proof where method calls are invoked or other instructions are performed which change the memory locations on the heap. If these method calls only change memory locations on the heap which do not affect those location on which the invariant at most depends on, it is still possible to use the stated properties of the invariant after such a method call. However, if the method calls also change location on the heap on which the invariant depends on, it is not possible to rely on those properties anymore and it has to be proven that the invariant still holds. For a more detailed description, see ⁸.

The Logic in Use

In this section, we make a short excursion to the formalism underlying the KeY tool. As we follow a deduction-based approach towards software verification, logics are the basic formalism used. More precisely, we use a typed first-order dynamic logic called JavaCardDL.

We do not intend here to give a formal introduction into the logic used, but we explain the intended meaning of the formulas. Furthermore, we assume that the reader has some basic knowledge of classical first-order logic.

In addition to classical first-order logic, dynamic logic has two additional operators called modalities, namely the diamond ${\langle\cdot\rangle{\cdot}}$ and box ${[\cdot]{\cdot}}$ modalities. Their first argument is a piece of JavaCard code and the second argument an arbitrary formula. Let $p$ be a program and $\phi$ an arbitrary formula in JavaCardDL. Then

• ${\langle p\rangle{\phi}}$ is a formula in JavaCardDL which holds iff program $p$ terminates and in its final state formula $\phi$ holds.

• ${[p]{\phi}}$ is a formula in JavaCardDL which holds iff if program $p$ terminates then in its final state formula $\phi$ holds.

The notion of a state is a central one. A state can be seen as a snapshot of the memory when running a program. It describes the values of each variable or field. A formula in JavaCardDL is evaluated in such a state.

Let $i,j$ denote program variables. Some formulas in JavaCardDL:

• The formula $i \doteq 0 \rightarrow \langle i = i + 1;\rangle i>0$ is a formula in JavaCardDL. The formual states:

  If the value of $i$ is $0$, then the program $i = i + 1;$ terminates and in the final state (the state reached after executing the program), the program variable $i$ is greater than $0$.

  The diamond operator states implicitly that the program must terminate normally, i.e., no infinite loops and recursions and no uncaught exceptions occur.

  Replacing the diamond in the formula above by a box $i \doteq 0 \rightarrow [i = i + 1;] i > 0$ changes the termination aspect and does not require that the program terminates, i.e., this formula is already satisfied if in each state where the value of $i$ is $0$ and if the program $i = i + 1;$ terminates then in its final state $i$ is greater than $0$.

• A typical kind of formula you will encounter is one with an update in front like

  $$\{ {i := a} ~~||~~ {j := b} \} ~\langle tmp = i; i = j; j = tmp; \rangle ~i \doteq b \wedge j \doteq a$$

  Intuitively, an update can be seen as an assignment, the two vertical strokes indicate that the two assignments $a$ to $i$ and $b$ to $j$ are performed in parallel (simultaneously). The formula behind the update is then valid if in the state reached executing the two "assignments", the program terminates (diamond!) and in the final state the content of the variables $i$ and $j$ have been swapped.

Sequents

Deduction with the KeY prover is based on a sequent calculus for a dynamic logic for JavaCard (JavaDL) ⁵⁹.

A sequent has the form $\phi_1, \ldots,\phi_m\;\vdash\;\psi_1,\ldots,\psi_n\; (m,n \geq 0)$, where the $\phi_i$ and $\psi_j$ are JavaDL-formulas. The formulas on the left-hand side of the sequent symbol $\;\vdash\;$ are called the antecedent and the formulas on the right-hand side are called the succedent. The semantics of such a sequent is the same as that of the formula $(\phi_1\land\ldots\land \phi_m) \to (\psi_1 \lor\ldots\lor \psi_n)$.

Proof-Obligations

In general, a proof obligation is a formula that has to be proved valid. When we refer to a proof obligation, we usually mean the designated formula occurring in the root sequent of the proof. A method contract for a method $m$ of a class $C$ consists in general of a

• precondition $pre$ describing the method-specific⁶ conditions which a caller of the method has to fulfill before calling the method in order to be guaranteed that the

• postcondition $post$ holds after executing the method and that the

• assignable/modifies clause $mod$ is respected. This means that at most the locations described by $mod$ are modified in the final state. In addition, we have a

• termination marker indicating if termination of the method is required. Termination required (total correctness) has the termination marker diamond, i.e. the method must terminate when the called in a state where the precondition is fulfilled. The marker box does not require termination (partial correctness), i.e., the contract must only be fulfilled if the method terminates.

In addition, each object $O$ has a possibly empty set of invariants $inv_{O}$ assigned to them.

For the general description, we refer to this general kind of contract. Mapping of JML specifications to this general contract notion is slightly indicated in Sect. 4.3{reference-type="ref" reference="sec:application"}. More details can be found in ⁶.

---

1. Gary T. Leavens, Erik Poll, Curtis Clifton, Yoonsik Cheon, Clyde Ruby, David Cok, Peter Müller, Joseph Kiniry, Patrice Chalin, and Daniel M. Zimmerman. Jml reference manual. Department of Computer Science, Iowa State University. Available from \url http://www.jmlspecs.org, July 2011. ↩↩↩

2. Gary T. Leavens, Albert L. Baker, and Clyde Ruby. Preliminary design of JML: a behavioral interface specification language for Java. Technical Report 98-06y, Iowa State University, Department of Computer Science, November 2004. See \url http://www.jmlspecs.org. URL: ftp://ftp.cs.iastate.edu/pub/techreports/TR98-06/TR.ps.gz. ↩↩

3. Steffen Schlager. Handling of Integer Arithmetic in the Verification of Java Programs. Master's thesis, Universität Karlsruhe, 2002. Available at: \url http://i12www.ira.uka.de/ key/doc/2002/DA-Schlager.ps.gz. ↩

4. Steffen Schlager. Symbolic Execution as a Framework for Deductive Verification of Object-Oriented Programs. PhD thesis, Fakultät für Informatik der Universität Karlsruhe, February 2007. ↩

5. Bernhard Beckert, Reiner Hähnle, and Peter H. Schmitt, editors. Verification of Object-Oriented Software: The KeY Approach. LNCS 4334. Springer-Verlag, 2007. ↩↩

6. Wolfgang Ahrendt, Bernhard Beckert, Richard Bubel, Reiner Hähnle, Peter H. Schmitt, and Mattias Ulbrich, editors. Deductive Software Verification - The KeY Book - From Theory to Practice. Volume 10001 of Lecture Notes in Computer Science. Springer, December 2016. ISBN 978-3-319-49811-9. doi:10.1007/978-3-319-49812-6. ↩↩↩

7. Christian Engel. A translation from jml to java dynamic logic. Studienarbeit, Fakultät für Informatik, Universität Karlsruhe, January 2005. ↩

8. Benjamin Weiß. Deductive Verification of Object-Oriented Software: Dynamic Frames, Dynamic Logic and Predicate Abstraction. PhD thesis, Karlsruhe Institute of Technology, 2011. ↩

9. Bernhard Beckert. A dynamic logic for the formal verification of Java Card programs. In I. Attali and T. Jensen, editors, Java on Smart Cards: Programming and Security. Revised Papers, Java Card 2000, International Workshop, Cannes, France, LNCS 2041, 6–24. Springer-Verlag, 2001. ↩